This is a brief summary of paper for me to study and simply arrange it, Adaptive Input Representations for Neural Language Modeling (Baevski and Auli., ICLR 2019) that I read and studied.

They pointed out the trouble for a substantional part of the overall computation in softmax, the common approach to lower the computation burden is to strcture the output vocabulary so that not all probabilities need to be computed.

Unlike the structure, the further method is adaptive softmax(Grave et al., arXiv 2017) which introduces a variable capacity scheme for output word embeddings, assigning more parameters to frequent words and fewer parameters to rare words.

So they applied the adaptive softmax into input embedding they called adative input embeddings which extend the adaptive softmax to input word representation.

This factorization assigns more capacity to frequent words and reduces the capacity for less frequent words with the benefit of reducing to rare words.

The adaptive softmax exploits the faction that the distrbution of word types in natural language follows a Zipfian distribution in order to imporves the computation of the output probabilities.

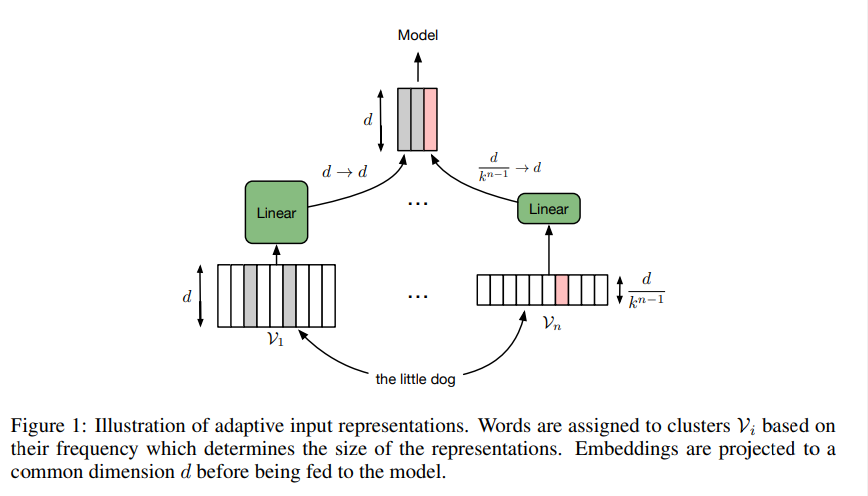
For adaptvie input embedding, they define a number of clusters that partitions the ferquency ordered vocbulary \(V = v_1 \cup v_2, …, v_{n-1} \cup v_n\) such that \(V_i \cap V_j = \emptyset\) for \( \forall i, j\) and \(i \neq j\), where \(v_1\) contains the most frequenc words and \(v_n\) the least frequenct words.

They reduce the capacity for each cluster which is that if words in \(v_1\) have dimension \(d\), then words in \(v_n\) have dimension \(\frac{d}{k^{n-1}}\). In their paper, they set up k as 4.

Next, they add linear projections \(W_1 \in \Bbb R^{d \times d}, …, W_n \in \Bbb R^{frac{d}{k^{n-1}} \times d} \) to map the embeddings of each cluster to dimension \(d\) so that the concatenated output of the adaptive input embedding layer can be easily used by the subsequent model as shown figure below:

Baevski and Auli., ICLR 2019

For detailed result about experiment, see their paper, Adaptive Input Representations for Neural Language Modeling (Baevski and Auli., ICLR 2019).

Note(Abstract): They introduce adaptive input representations for neural language modeling which extend the adaptive softmax of Grave et al. (2017) to input representations of variable capacity. There are several choices on how to factorize the input and output layers, and whether to model words, characters or sub-word units. They perform a systematic comparison of popular choices for a self-attentional architecture. Their experiments show that models equipped with adaptive embeddings are more than twice as fast to train than the popular character input CNN while having a lower number of parameters. On the WIKITEXT-103 benchmark they achieve 18.7 perplexity, an improvement of 10.5 perplexity compared to the previously best published result and on the BILLION WORD benchmark, they achieve 23.02 perplexity

Download URL:
The paper: Adaptive Input Representations for Neural Language Modeling (Baevski and Auli., ICLR 2019)

Reference

Paper
- arXiv Version: Adaptive Input Representations for Neural Language Modeling (Baevski and Auli., arXiv 2019)
- ICLR Version: Adaptive Input Representations for Neural Language Modeling (Baevski and Auli., ICLR 2019)
How to use html for alert
- how to use icon
For your information

Adaptive Input Representations for Neural Language Modeling

Title of paper - Adaptive Input Representations for Neural Language Modeling

Adaptive Input Representations for Neural Language Modeling

Title of paper - Adaptive Input Representations for Neural Language Modeling

Reference