This is a brief summary of paper for me to note it, On the Properties of Neural Machine Translation: Encoder-Decoder Approaches (Cho et al., SSST-WS 2014)
They analyzed the properties of machine translation model based on neural network.
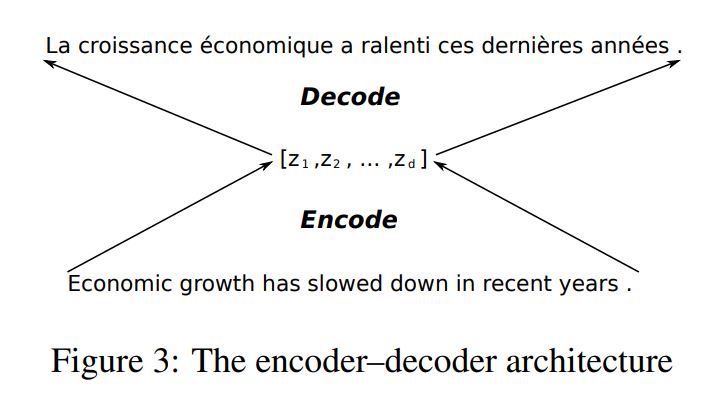
Since most of neural-netwrok-based translation model is sequence-to-seqeunc model, the translation model has a encoder and a decoder.
Encoder summarize input sentence (source sentence) into a fixed-length vector and Decoder generate output sentence (target sentence).
To sum up their results. When the number of unkown words and the length of sentence increase, the performance is degraded.
Above all, before entering to what kind of encoder they use, note that they use an RNN with gated hidden units (GRU) as a decoder.
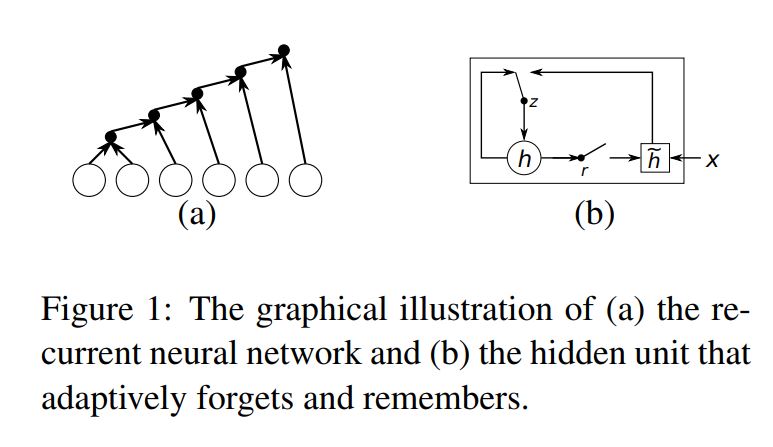
Let’s see the Recurrent Neural Network with Gated Hidden Neurons.
A recurrent neural network works on a variable-length sequence \(x = (x_1,X_2,…,X_T)\) by maintaining a hidden state h over time. At each timestip t, the hidden state \(h^{(t)}\) is updated by:
\[h^{t} = f(h^{t-1}, x_t)\]where f is an activation function. Often f is as simple as performing a linear transformation on the input vectors, summing them, and applying an element-wise logisitic sigmoid function.
They used new activation fucntion which augments the usual logisitc sigmoid activation function with two gating units called reset gate, r and update gate, z. Each gate depends on the previous hidden state \(h^{t-1}\), and the current intput , \(x_t\) controls the flow of information.
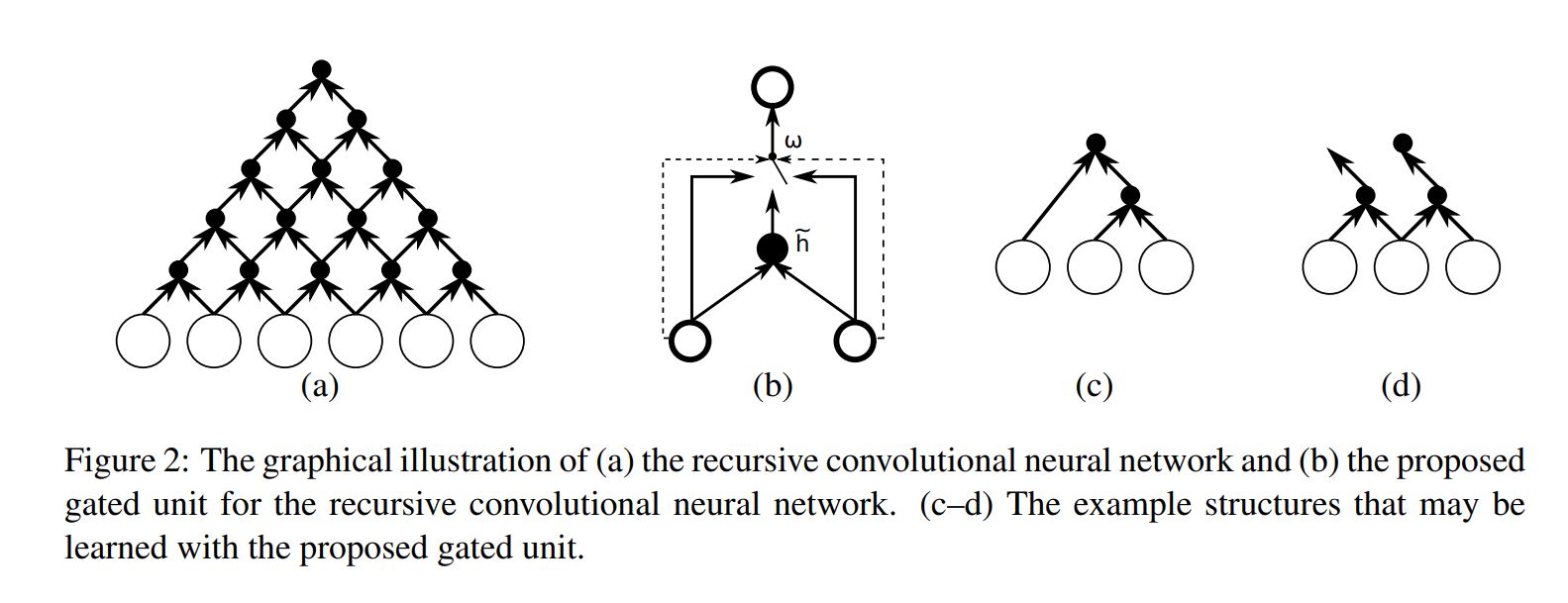
Let’s see the Gated Recursive Convolutional Neural Network.
They also introduce a new binary convolutional neural network whose weights are recursively applied to the input sequence until it outputs a single fixed-length vector.
Let \(x = (x_1, x_2, … , X_T) \) be an input sequence, where \(x_t \in \mathbb{R^d}\). The proposed gated recursive convolutional neural network consists fo four weight matrices \(W^l, W^r, G^l\) and \(G^r\). At each recursion level \(t \in [1, T-1]\), the activation of the j-th hidden unit \(h_j^{t}\) is computed by:
\[\begin{matrix} h_j^{(t)} = w_c\bar{h_j^{(t)}} + w_lh_{j-1}^{(t-1)} + w_rh_j^{(t-1)} & (1) \end{matrix}\]where \(w_c, w_l\) and \(w_r\) are the values of a gater that sum to 1. The hidden unit is initialized as
\[\begin{matrix} h_j^{(0)} = Ux_j & (2) \end{matrix}\]Where U projects the input into a hidden space.
The new activation \(\bar{h_j^{t}}\) is computed as usual :
\[\begin{matrix} \bar{h_j^{(t)}} = \sigma(W^lh_{j-1}^{(t)} + W^rh_j^{(t)}) & (3) \end{matrix}\]Where \(\sigma\) is an element-wise nonlinearity.
The gating coefficients \(w’s\) are computed by:
\[\begin{bmatrix} w_c \\ w_l \\ w_r \\ \end{bmatrix} = \frac{Z}{1}exp(G^lh_{j-1}^{(t)} + G^rh_j^{(t)})\]Where \(G^l, G^r \in \mathbb{R^{3xd}}\) and Z is normalized term :
\[\begin{matrix} Z = \sum_{k=1}^{3}[exp(G^lh_{j-1}^{(t)} + G^rh_j^{(t)})]_k & (3) \end{matrix}\]According to this activation, one can think of the activation of a single node at recursion level t as a choice between either a enw activation computed from both left and right children, the activation from the left child, or the activation from right child.
The choice allows the overal structure of the recursive convolution to change adaptively with respect to an input sample.
When they generate target sentence, they use a basic form of beam-search to find a translation that maximizes the conditional probability given by a specific models.
it is better than Greed search.
If you want to know what beam-search is, see the following (e.g. Youtube lecture)
The paper: On the Properties of Neural Machine Translation: Encoder-Decoder Approaches (Cho et al., SSST-WS 2014)
Reference
- Paper
- How to use html for alert
- For your information