This is a brief summary of paper for me to study and note it, Skip-Thought Vectors (Kiros et al., NIPS 2015).

This papre is related to how to representation a sentence to a fixed-size vector utilizing sequence to sequence model with GRU.

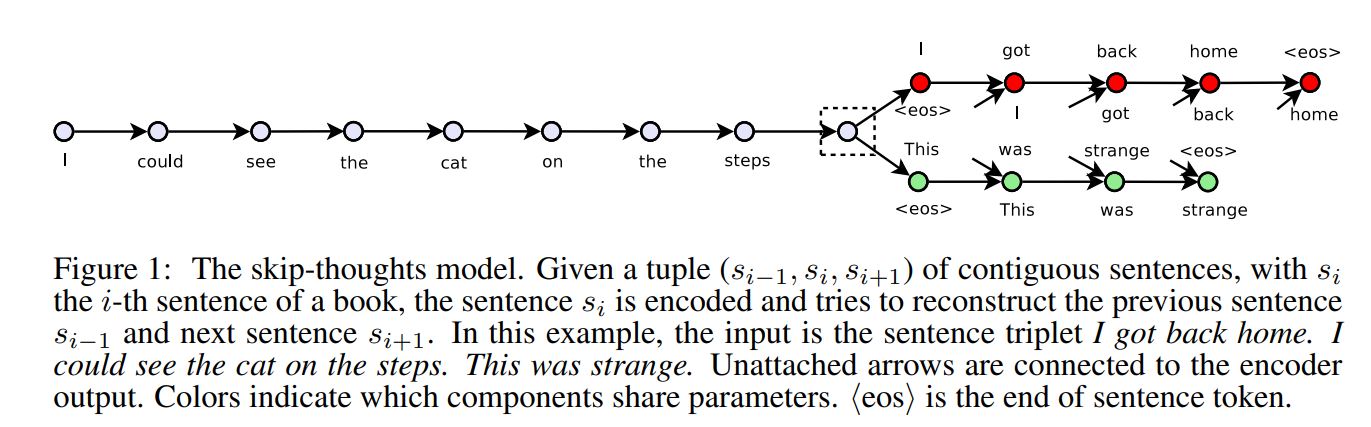
Kiros et al., NIPS 2015

They model use a sentence tuple $(s_{t-1}, s_t, s_{t+1})$ . Let $w_i^t$ denote the t-th word for sentence $s_i$ and let $x_i^t$ denote its word embedding.

From here, I describe their model in three parts: the encoder, decoder, and objective function.

Encoder. Let $w_i^1, … , w_i^N$ be the words in sentence $s_i$ where N is the number of words in the sentence. At each time step, the encoder produces a hidden state $h_i^t$ which can be interpreted as the representation of the seqeuence $w_i^1, … , w_i^t$ . The hidden state $h_i^N$ thus represents the full sentence.

To encode a sentence, they iterate the following sequence of equations (dropping the subscript i):

$\begin{matrix} r^t = \sigma(W_rx^t + U_rh^{t-1}) & (1) \end{matrix}$

$\begin{matrix} z^t = \sigma(W_zx^t + U_zh^{t-1}) & (2) \end{matrix}$

$\begin{matrix} \bar{h^t} = tanh(Wx^t + U(r^t \bigodot h^{t-1})) & (3) \end{matrix}$

$\begin{matrix} h^t = (1-z^t) \bigodot h^{t-1} + z^t \bigodot \bar{h^t} & (4) \end{matrix}$

where $\bar{h^t}$ is the proposed state update at time t, $z^t$ is the update gate, $r^t$ is the reset gate ( $\bigodot$ ) denotes a component-wise product. Both update gates takes values between zero and one.

Decoder. The decoder is a neural language model which conditions on the encoder output $h_i$ . The computation is similar to that of the enocoder except we introduce matrices $C_z, C_r$ and $C$ that are used to bias the update gate, reset gate and hidden state computation by the sentence vector. One decoder is used for the next sentence $S_{i+1}$ while a second decoder is used for the previous sentence $s_{i-1}$ . Separate parameters are used for each decoder with the exception of the vocabulary matrix V, which is the weight matrix connecting the decoder’s hidden state for computing a distribution over words.

They describe the decoder for the next sentence $s_{i+1}$ although an analogous computation is used for the previous sentence $s_{i-1}$ . Let $h_{i+1}^t$ denote the hidden state of the decoder at time t. Decoding involves iterating through the following sequence of equations (dropping the subscript i+1):

$\begin{matrix} r^t = \sigma(W_r^dx^t + U_r^dh^{t-1} + C_rh_i) & (5) \end{matrix}$

$\begin{matrix} z^t = \sigma(W_z^dx^t + U_z^dh^{t-1} + C_zh_i) & (6) \end{matrix}$

$\begin{matrix} \bar{h^t} = tanh(Wx^t + U(r^t \bigodot h^{t-1}) + Ch_i) & (7) \end{matrix}$

$\begin{matrix} h^t = (1-z^t) \bigodot h^{t-1} + z^t \bigodot \bar{h^t} & (8) \end{matrix}$

Given $h_{i+1}^t$ , the probability of word $w_{i+1}^t$ given the previous t-1 words and the encoder vector is

$\begin{matrix} P(w_{i+1}^t | w_{i+1}^{<t}, h_i) \propto exp(v_{w_{i+1}^t}h_{i+1}^t) & (9) \end{matrix}$

where $h_{i+1}^t$ denotes the row of V corresponding to the word of $w_{i+1}^t$ . An analogous computation is performed for the previous sentence $S_{i-1}$

Objectiv. Given a tuple ( $s_{i-1}, s_i, s_{i+1}$ ), the objective optimized is the sum of the log-probabilities for the forward and backward sentences conditioned on the encoder representation:

$\begin{matrix} \sum_{t}log(P(w_{i+1}^t | w_{i+1}^{<t}, h_i)) + \sum_{t}log(P(w_{i-1}^t | w_{i-1}^{<t}, h_i)) & (10) \end{matrix}$

The total objective is the above summed over all such training tuples.

The evaluation tasks.
- Semantic relatedness on the SemEval 2014 Task 1 (Marelli et al., 2014)
- Paraphrase detection on the Microsoft Research Paraphrase Corpus (Dolan et al., 2004)
- Image-Sentence ranking on the Microsoft COCO dataset (Lin el al., 2014): They consider two task. e.g. One is image annotation and the other image search
- Classification benchmarks on 5 datasets: movie review sentiment (MR), customer product reviews (CR), subjectivity/objectivity classification (SUBJ), opinion polarity (MPQA) and question-type classification (TREC).

Note(Abstract): They describe an approach for unsupervised learning of a generic, distributed sentence encoder. They train an encoder-decoder model that tries to reconstruct the surrounding sentences of an encoded passage. Sentences that share semantic and syntactic properties are thus mapped to similar vector representations. They also introduce a simple vocabulary expansion method to encode words that were not seen as part of training, allowing them to expand their vocabulary to a million words. In order for them to evaluate their vectors with linear models on 8 tasks: semantic relatedness, paraphrase detection, image-sentence ranking, question-type classification and 4 benchmark sentiment and subjectivity datasets.

Download URL:
Skip-Thought Vectors (Kiros et al., 2015)

Reference

Paper
- arXiv Version: Skip-Thought Vectors (Kiros et al., arXiv 2015)
- NIPS Version: Skip-Thought Vectors (Kiros et al., NIPS 2015)
How to use html for alert
- how to use icon
For your information

Skip-Thought Vectors

Title of paper - Skip-Thought Vectors

Skip-Thought Vectors

Title of paper - Skip-Thought Vectors

Reference