This post is a brief summary about the paper that I read for my study and curiosity, so I shortly arrange the content of the paper, titled Fine-Tuning Langauge Models from Human Preferences (Ziegler et al., arXiv 2020), that I read and studied.

They said that the existing RL method has been appiled to the simulated enviroment. However, they wanted to apply RL into real-word tasks which expresses complex information about value as natural languages.

They said that there is a long literature applying reinforcement learning to natural language tasks. The most works uses algorithmically defined reward functions such as BLEU for translation, ROUGE for summarization, music theory-based rewards, or event detectors for story gneration.

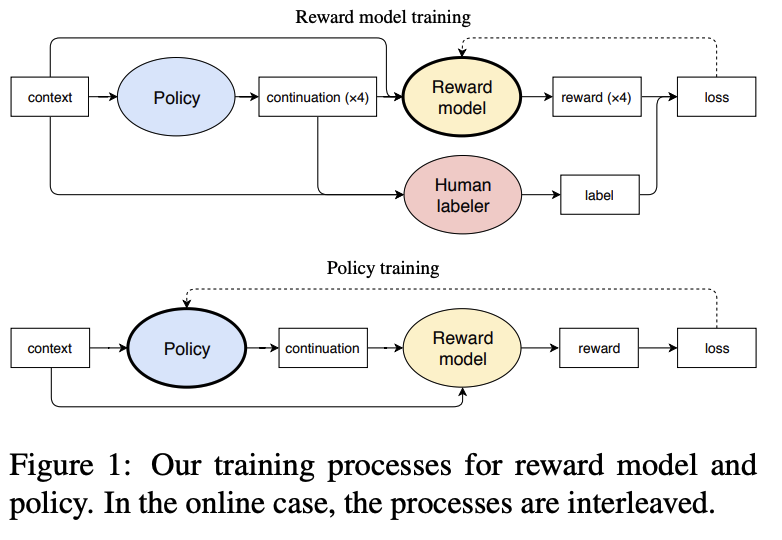
Ziegler et al., arXiv 2020

Let’s see preference option $(y_1, y_2, y_3, y_4)$, prompt $x$, and $b \in {0,1,2,3}$. Having collected a dataset $S$ of $(x, y_0, y_1, y_2, y_3, b)$ tuples, the reward model is fitted as follows:

\[loss(r) = E_{(s, \{y_i\}, b) \sim S}[log(\dfrac{e^{r(x, y_b)}}{\sum_{i} e^{r(x, y_i)}})]\]

They perform RL with a penalty with expectiona $\beta KL(\pi, \rho)$ using the following loss:

\[R(x,y) = r(x,y) - \beta log(\dfrac{\pi(y|x)}{\rho(y|x)})\]

Their overal training process is:

  1. Gather samples $(x, y_0, y_1, y_2, y_3)$ via $x \sim D , y_i \sim \rho(. x)$. Ask humans to pick the best $y_i$ from each.
  2. Initailize $r$ to $\rho$, using random initialization for the final linear layer of $r$. Train $r$ on the human samples using loss of reward model.
  3. Train $\pi$ via Proximal Policy Optimization (PPO) with reward $R$ from RL training with a penality on $x \sim D$.
  4. In the online data collection case, continue to collect additional samples, and periodically retrain the reward model $r$.

For detailed experiment and explanation, refer to the paper, titled Fine-Tuning Langauge Models from Human Preferences (Ziegler et al., arXiv 2020)

Reference