This is a brief summary of paper for me to study and organize it, SpanBERT: Improving Pre-training by Representing and Predicting Spans (Joshi et al., TACL 2019) that I read and studied.

They said that

pre-training methods like BERT have shown strong performance gains using self-supervised training that masks individual words or subword units. However, many NLP tasks involve reasoning about relationships between two or more spans of text.

So they proposed the SpanBERT, a pre-training method that is designed to better represent and predict spans of text. It differs from the BERT in the masking scheme and the training objectives.

  • The masking scheme: masking randome contiguous spans rather than random individual tokens using geometric distribution.

  • The training objectives: using a novel span-boundary objective(SBO) to train model to predict the entire masked span from the observed tokens at its boundary.

In other words, they observed that single-sentence trining works considerably better than bi-sequence training with next sentence prediction (NSP), thus the extend the BERT in masking sheme and training objectives as follow:

Joshi et al., TACL 2019

They modified two training schemes, which is maked language model (MLM) and next sentence prediction (NSP), in BERT.

For MLM also known as a cloze task, given a seuqence of words or sub-word tokens \(X = (x_1, …, x_n)\), MLM is a task to predict missing tokens in a sequence.

to train MLM in BERT, when a subset of tokens \(Y \subseteq X\) is sampled and subsituted with a different set of tokens, Y accounts for 15% of the tokens in \(X\); of those, 80% are replaced with [MASK], 10% are replaced with a random token (according to unigram distribution), and 10% are kept unchanged.

The BERT predicts the original tokens in \(Y\) from the modified input.

When they train SpanBERT, as in BERT, they also mask 15% of input tokens in total: subsitituting 80% of the masked tokens with [MASK], 10% with random tokens, and 10% with the original tokens. However, they perform this masking scheme as span-level and no for each token individually.

When sampling the spans of text, they sample the span’s length from a geometic distribution in not subwords tokens but a sequence of complete words.

For NSP known as predicting whether two sequences \(X_A, X_B\) is direct continuation, they remove the NSP from SpanBERT, instead they sample a single full-length sequence (i.e. a single contingous segment) up to \(n=512\) tokens, rather than two half-segments that sum up to n tokens together in BERT.

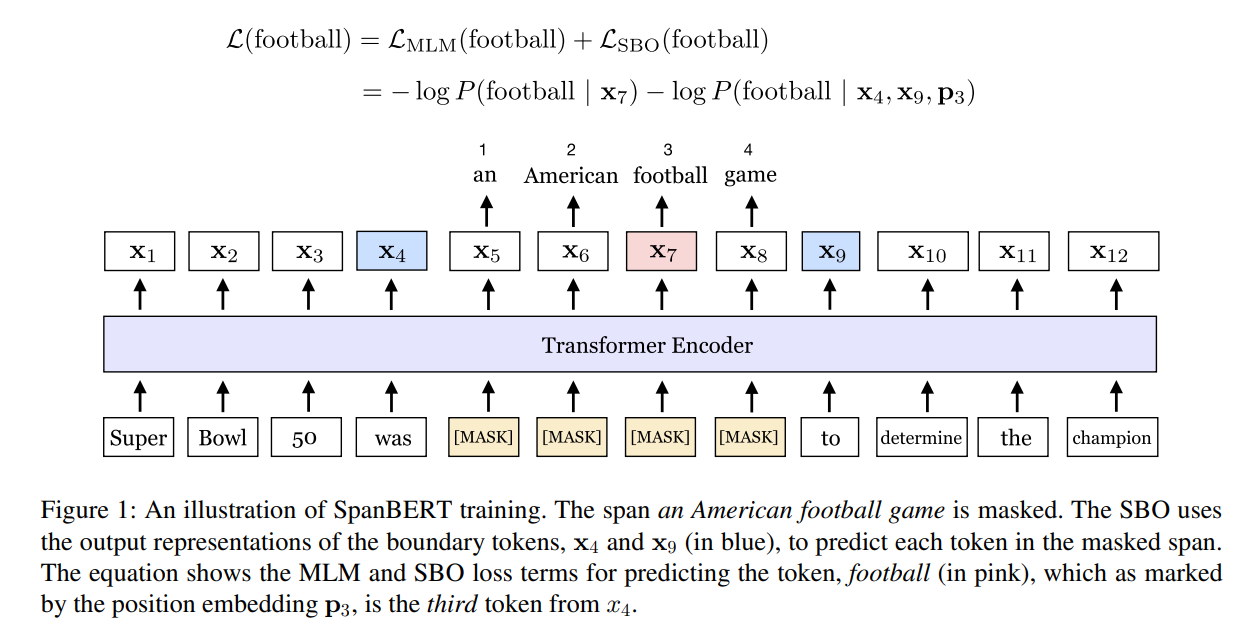
In addition to those, They introduced the Sapn boundary Objective (SBO).

inspired span selection models makeing a fixed-length representation of a span using its boundary tokens (start and end token), they used a span represenation with start and end token.

since they want to make the span representation summarize as much of the internal span content as possible, they introduce a span boundary objective that involves predicting each token of a masked span using the external boundary tokens \((x_{s-1}, x_{e+1})\) in a masked span and the position embedding \(p_i\) of the target token .

Specifically, given a masked span \(((x_s, … x_e) \in Y\), where \((s,e)\) indicates its start and end position, the span reprensentation is :

\[y_i = f(x_{s-1}, x_{e+1}, p_i)\]

In their work, they used represenation function \(f(\cdot)\) as a 2-layer feed-forward network with GeLU activations.

In their experiment, they found those trends:

  • The next sentence prediction(NSP) in BERT’s pre-training objectives hurt the performance on downstream tasks comparing with single sentence BERT(in Section 6.2).

  • the improvement factors of the performance in SpanBERT:

    • Masking contiguous random spans than rather than random tokens.

    • Training the span boundary representations to predict the entire content of the masked span, without relying on the individual token representation within it.

For detailed experiment analysis, you can found in SpanBERT: Improving Pre-training by Representing and Predicting Spans (Joshi et al., TACL 2019)

Reference