This is a brief summary of paper for me to study and organize it, End-to-end Neural Coreference Resolution (Lee et al., EMNLP 2017) that I read and studied.
They proposed end-to-end coreference resoultion method based on neural network architecture as follows:
When they tried to resolve coreferecne resolution task based on neural network, They defined the task with some set-up like:
First, formulatint the task of end-to-end coreference resolution as a set of decisions for every possible span in the document.
-
The input is a document \(D\) containing \(T\) words along with metadata such as speaker and genre information.
-
They limited the number of spans like \(N = frac{T(T+1)}{2}\) to be the nubmer of possible text spans in \(D\).
-
They used annotations such that the start and end indices of a span \(i\) in \(D\) respectively by START(\(i\)) and END(\(i\)), for \(1 ≤ i ≤ N\).
Second, for dataset We sorted an ordering of spans based on START(\(i\)); spans with the same start index are ordered by END(\(i\)).
Since The task is to assign to each span i an antecedent \(y_i\), third, they set the set of possible assignments for each \(y_i\) is \(Y(i) = {\epsilon, 1, . . . , i − 1}\), a dummy antecedent \(\epsilon\) and all preceding spans.
- The true antecedents of span \(i\), i.e. span j such that \(1 ≤ j ≤ i − 1\), represent coreference links between \(i\) and \(j\).
For the dummy antecedent \(\epsilon\), it is defined for two scenarios in their configuration for the coreference resoultion task.
(1) the span is not an entity mention (2) the span is an entity mention but it is not coreferent with any previous span.
These decisions implicitly define a final clustering, which can be recovered by grouping all spans that are connected by a set of antecedent predictions.
For model, they aim to learn a conditional distribution \(P(y_1,…,y_n|D)\) which produces the correct clustering. They use a product of multinomial for each span:
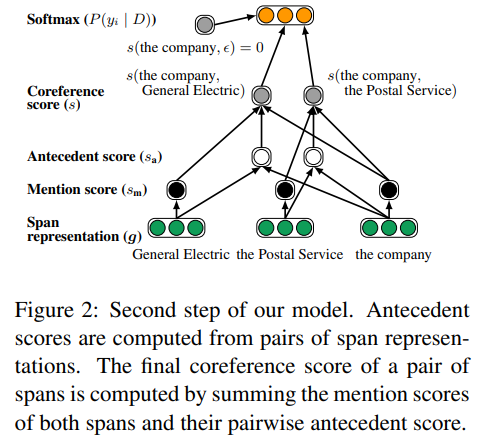
\[p(y_1,...,y_n\|D) =\prod_{i=1}^n P(y_i|D) =\prod_{i=1}^n \frac{exp(s(i,y_i)}{\sum_{y'\in y(i)}exp(s(i,y'))}\]where \(s(i,j)\) is pairwise score for a coreference link between span \(i\) and span \(j\) in document \(D\).
For the pairwise coreference score, there are three factors:
(1) whether span \(i\) is a mention (2) whether span \(j\) is a mention (3) whether \(j\) is an antecedent of \(i\)
So the total pairwise score :
\[s(i,j) = \begin{cases} 0, & \text{j =} \epsilon \\ s_m(i)+s_m(j)+s_a(i,j), & \text{j !=} \epsilon \end{cases}\]Where \(s_m(i)\) is a unary score for span i being a mention, and \(s_a(i,j)\) is pairwise score for span j being an antecedent of span \(i\).
According to the exquation of pairwise score above, the computation architecture is as follows:
With span representation \(g_i\), they compute pairwise score function via standard feed-forward neural networks(FFNN):
\[s_m(i) = w_m \bullet FFNN_m(g_i)\] \[s_a(i,j) = w_a \bullet FFNN_a(g_i,g_j,g_i \circ g_j, \varnothing(i,j))\]where \(\bullet\) denotes the dot product, \(\circ\) denotes element-wise multiplication, and FFNN denote a feed-forward neural network that computes a non-linear mapping from input to output vectors.
The antecedent scoring function \(s_a(i,j)\) includes explicit element-wise similarity of each span \(g_i \circ g_j\) and a feature vector \(\varnothing(i,j)\) encoding speaker and genre information form the metadata and the distance between the two spans.
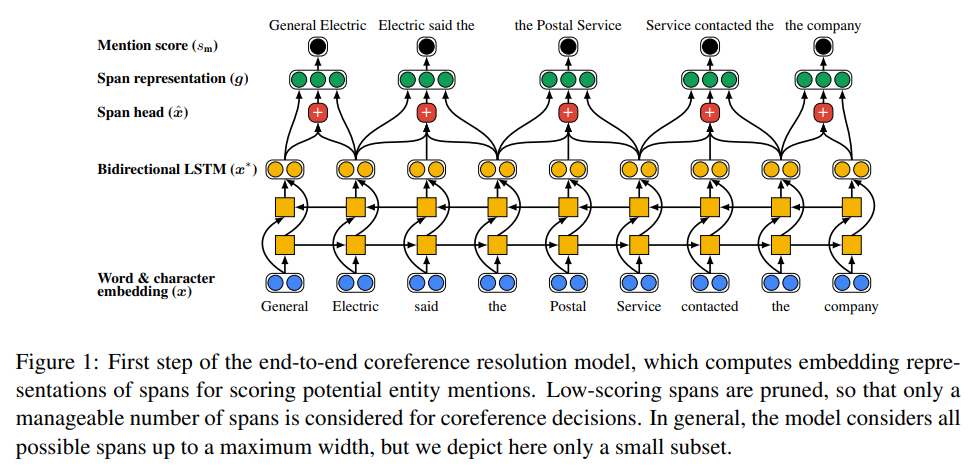
For Span representation, They used bidirectional LSTM and attention mechanism in in each span to model each head words.
Finally, they produced the final representation \(g_i\) of span \(i\)
\[g_i = [x_{START(i)}^{*},x_{END(i)}^{*},\hat x_i, \varnothing(i)]\]This only include the boundary representation \(x_{START(i)}^{*}\) and \(x_{END(i)}^{*}\). they introduce soft head word vector \(\hat x_i\) and a feature vector \(\varnothing(i)\) encoding the size of span \(i\).
where \(\hat x_i\) is a weighted sum of word vectore in span \(i\) by using attention mechanism, \(x_{START(i)}^{*}\) and \(x_{END(i)}^{*}\) is the concatenated output of bidirectional LSTM on start’s and end’s index respectively in span \(i\).
For detailed experiment analysis, you can found in End-to-end Neural Coreference Resolution (Lee et al., EMNLP 2017)