This is a brief summary of paper for me to study it, Effective Approaches to Attention-based Neural Machine Translation (Luong et al., EMNLP 2015)

The reason that I am writing this post is for me to organize about studying what the Attention is in deep learning.

Machine Translation task is one of natural language understanding and has been hard to improve the performance.

However, after using neural network on Machine Translation task. The performance of MT start outperforming the conventional phrase-based translation.

So the authors used additive attention to improve the performance of NMT.

The reason they used additive attention is it is difficult to include all information of a source sentence into a fixed-length vector as a context vector.

In order to resolve the problem using a fixed-length vector, they used soft-alignment jointly learning alignment and translation.

From a probabilistice perspective, translation is eqaul to find a target sentence y that maximizes the conditional probability of y given a source sentence x.

\[\hat{y} = \underset{y}{\mathrm{argmax}} P(y|x)\]

In the equation above,

  • x is a source sentence
  • y is a target sentence
  • P(y|x) is the conditional probabliity of y given x.

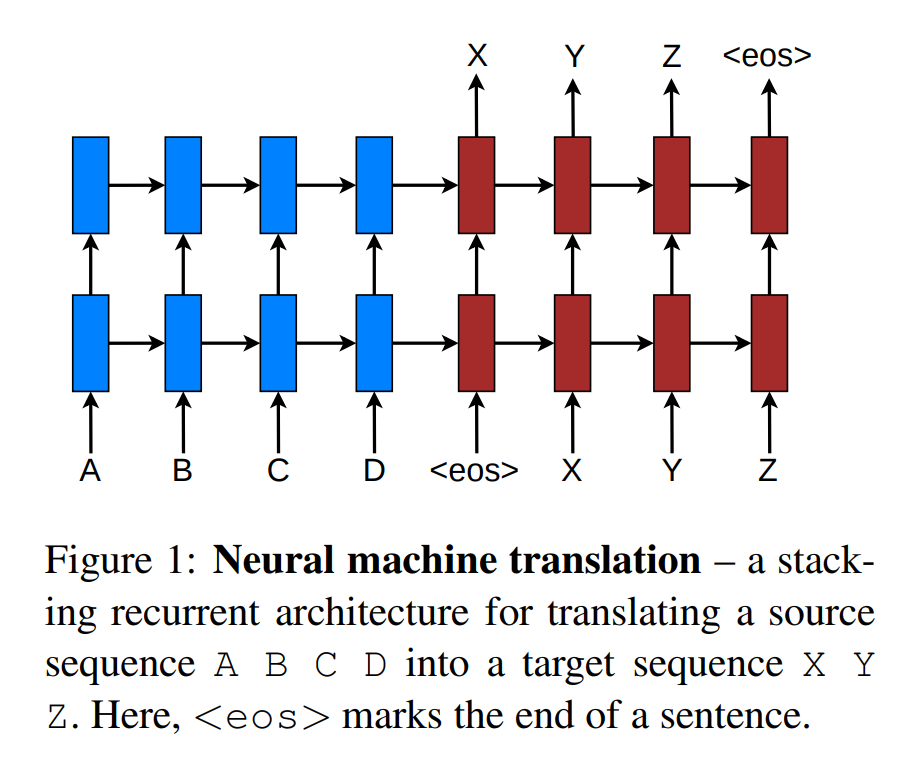
Luong et al.(2016)

They suggested two attention machanisms. one is the global attention mechanism and the other is the local attention mechanism which is new attention mechanism.

local attention mechanism considers the trade-off between soft and hard vesrion attention model proposed by Xu et al. (2015)

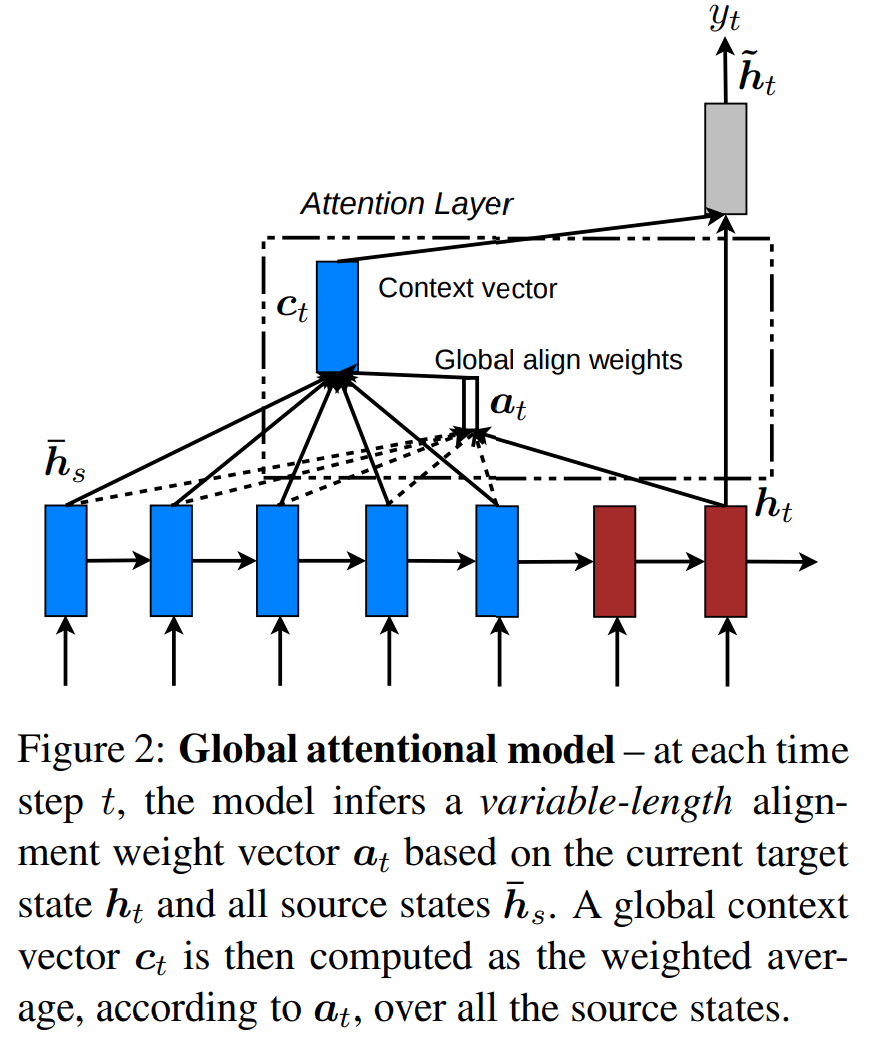
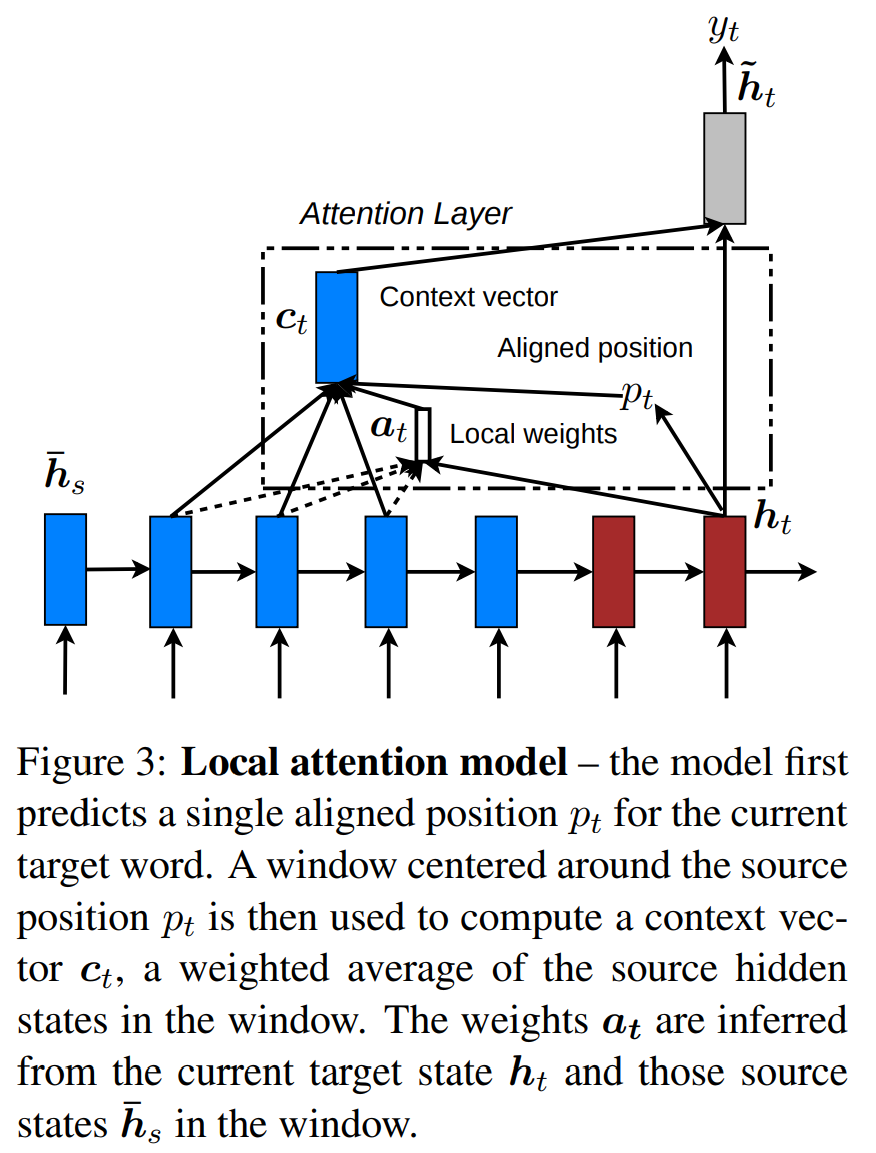
Global attention model by Luong et al.(2016) Local attentio model by Luong et al.(2016)

They proposed three formulas which caculate aligment scores with a content-based funtion.

\[a_t(s) = align(h_t, \bar{h}_s) = \frac{exp(score(h_t, \bar{h}_s))}{exp(\sum_{s'}score(h_t, \bar{h}_{s'})}\] \[score(h_t, \bar{h}_s)= \begin{Bmatrix} h^T_t \bar{h}_s && dot \\ h^T_t W_a\bar{h}_s && general \\ v^T_a tanh(W_a[h_t;\bar{h}_s] && concat\\ \end{Bmatrix}\]

Another one is a location-based funtion

\[\begin{matrix} a_t = softmax(W_ah_t) && location\end{matrix}\]

Reference