This article is just brief summary of Character-Aware Neural Language Models (Kim et al., AAAI 2016) and posting for me to study what the memory network is.

Their neural network consists of CNN for character-level as input, also high-way network before LSTM and finally LSTM-LM(Language model).

A Statical Languae model is probability distribution over sequences of words. Given such a sequence like of length m, LM assigns a probability \( P(w_{1}, ……. , w_{m}) \) to the whole sequence.

This task of Language model on Natural Languge is difficult, becuase there is no specification of the usages of natural Language.

Or another definition of LM is probabilistic that are able to predict the next word in the sequence given the words that precede it.

the definition that LM predicts the next words given a sequence of words is from Machine Learning Mastery

let’s say the length of a sequence is 3, if we want to predict fourth word. the pobability of next word is conditional probability distribution is like :

  • \( P(w_{3} | w_{1}, w_{2}) = P(w_{1})*P(w_{2}|w_{1})*P(w_(3)|w_{1}, w_{2}) \)

they estimate the probability of LM withe their model.

Let’s see their model!!

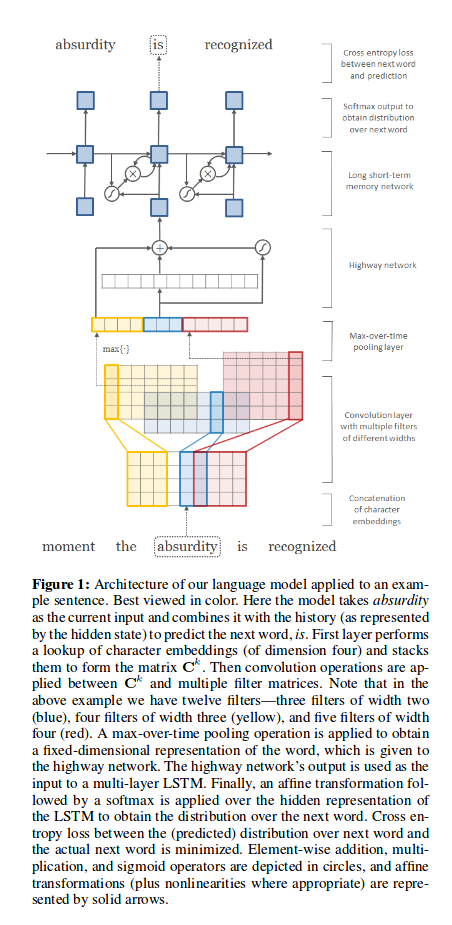
Kim et al., AAAI 2016

They used CNN, Highway network and LSTM.

in particular, Let’s see the highway network, recently proposed by Srivastava et al.(2015).

one layer of a highway nework does the following :

  • \( z = t \odot g(W_{H}y + b_{H}) + (1 - t) \odot y \) where g is a nonliearity.

  • \( t = \sigma(W_{T}y + b_{T}) \) is called tranform gate, and (1 - t) is called carry gate.

Also let’s the result of Learned word representation

Word embeddings obtained through NLMs show you the property whereby semantically close words are likewise close in the induced vector space.

Let’s see the figure below with this intution about Word embeddings.

Also, I realized What the hierarchical softmax is.

Let’s see the hierarchical softmax they used

they pcik the number of cluster \( c = \lceil \sqrt{|V|} \rceil \), and randomly split \( V \) into mutually exclusive and collectively exhastive subsets \( V_{1}, ……. , V_{c} \) of approximately equal size.

\( F(x) = \frac{exp(h_{t} \cdot s^r + t^r)}{\sum_{r^{`}=1}^n exp(h_{t} \cdot s^{r^{`}} + t^{r^{`}})} \)

\( G(x) = \frac{exp(h_{t} \cdot P_{r}^j + q_{r}^j)}{\sum_{j^{`} \in V_{r}} exp(h_{t} \cdot P_{r}^{j^{`}} + q_{r}^{j^{`}})} \)

The \( Pr(W_{i+1} = j | W_{1:t}) = F(x) \times G(x) \)

Wherer r is the cluster index such that \( j \in V_{r} \). The first term is imple the porbability of picking cluster r, and the second term is the probability of picking word j given that cluster r is picked.

Reference