This post is a brief summary about the paper that I read for my study and curiosity, so I shortly arrange the content of the paper, titled Self-Attention with Relative Position Representations, Shaw et al., NAACL 2018, that I read and studied.

The original paper(Vaswani et al. NIPS 2017) for transformer architecture uses position encoding in input layer. On the contrary, this paper proposes the relative position embedding in the internal structure of transformer.

how they incorporate the relative position embedding in the transformer structure is as follows:

For value embedding section,

\[z_i = \sum_{j=1}^n \alpha_{ij}(x_j W^V + a_{ij}^V)\]

For key embedding section,

\[e_{ij} = \frac{x_i W^Q (x_j W^K + a_{ij}^K)^T}{\sqrt d_z}\]

As you can see Figure 1 below, they used the relative position encoding on key and value vectors.

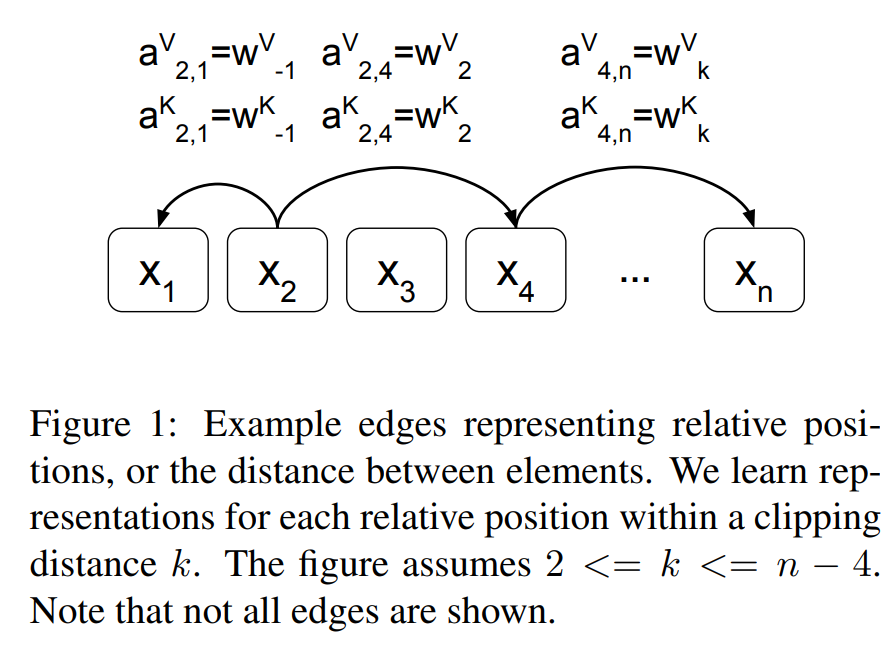
Shaw et al. NAACL 2018

For detailed explanation of the above equations, refer to the paper, titled Self-Attention with Relative Position Representations, Shaw et al., NAACL 2018.

Since they extend self-attention to take account of the pairwise relationships between input elements, they model the input as a labeled, directed, and fully connected graph.

They don’t consider all of the relative positions in a input sequence, so they learn representations for each relative position within a clipping distance K.

They hypothesized the precise relative position information is not useful beyond a certain distance clipped.

Reference