This is a brief summary of paper for me to study and arrange it, Bag-of-Embeddings for Text Classification (Jin et al., IJCAI 2016) I read and studied.
They thought One useful feature beyond bag-of-words as bag-of-ngrams.
In particular, they said bigrams offer a certain degree of compositionality while being relatively less sparse compared with larger n-gram features in their paper with text below:
For example, the bigram “abnormal return” strongly indicates finance, although both “abnormal” and “return” can be common across difference classes. Similar examples include “world cup” and “large bank”, where bi-grams indicate text classes, but the words do not.
One intuitive reason behind the strength of bigrams is that they resolve the ambiguity of polysemous words. In the above examples the words ”return”, ”cup”, and ”bank” have different meanings under different document classes, and the correct identification of their word sense under a ngram context is useful for identifying the document class. For example, when the word ”bank” exists under a context with words such as ”card” and ”busy”, it strongly indicates the ”finance” sense. This fact suggests a simple extension to bag-of-word features by incorporating context and word sense information. We propose a natural extension to the skip-gram word embedding model.
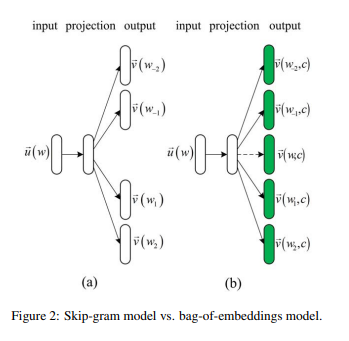
With article above, They proposed bag-of-embedding by exploiting using multi-prototype word embedding as follows:
As you can see image above, they are different from the skip-gram model in the definition of target and context embeddings in that the target embeddings are class-dependent, and each word can have different target embeddings in different classes. On the other hand, each word has a unique context embedding across classes.
While based on Skip-gram model, on constrary to handling input on original Skip-gram model, they used context vector as input and target vector as output.
For a text classifier, they bulit by using a Naive Bayes model with bag-of-embeddings probabilities.
Their result showed the bag-of-embedding model exploits contextual information by deriving the probabilities of class-sensitive embedding vectors from their inner product with context words.