this refers to 윤성우의 열혈 자료구조.
1-1. What is Exprssion Tree???
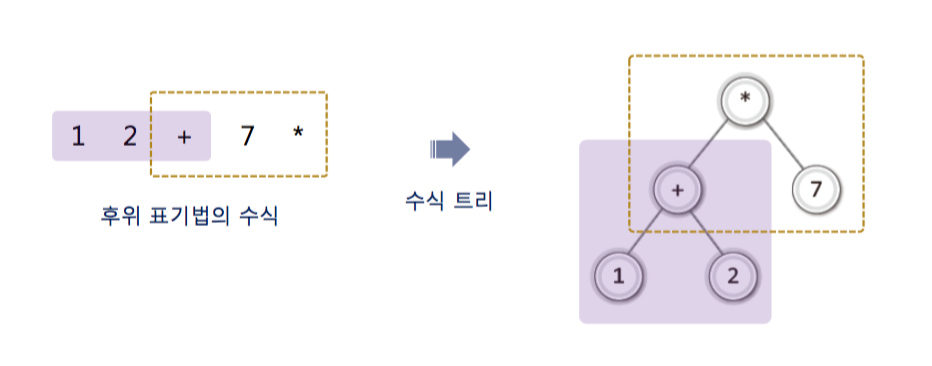
- 수식 트리란 말 그대로 수식을 트리로 표현을 하는 것을 말한다.
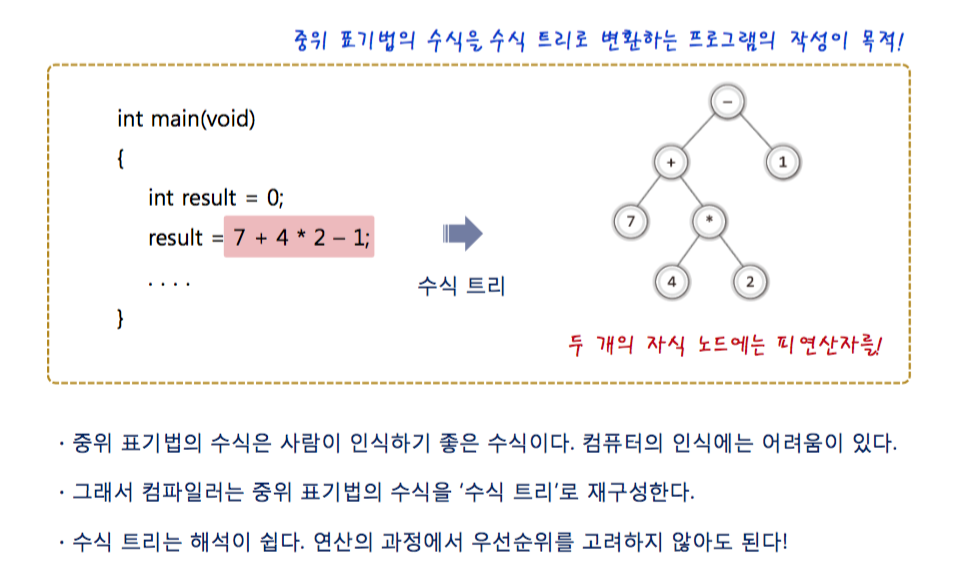
- 다음 수식 트리를 가지고 연산하는 과정이다.
- 수식 트리에서 자식은 피연산자라는 사실 !!!!!!!
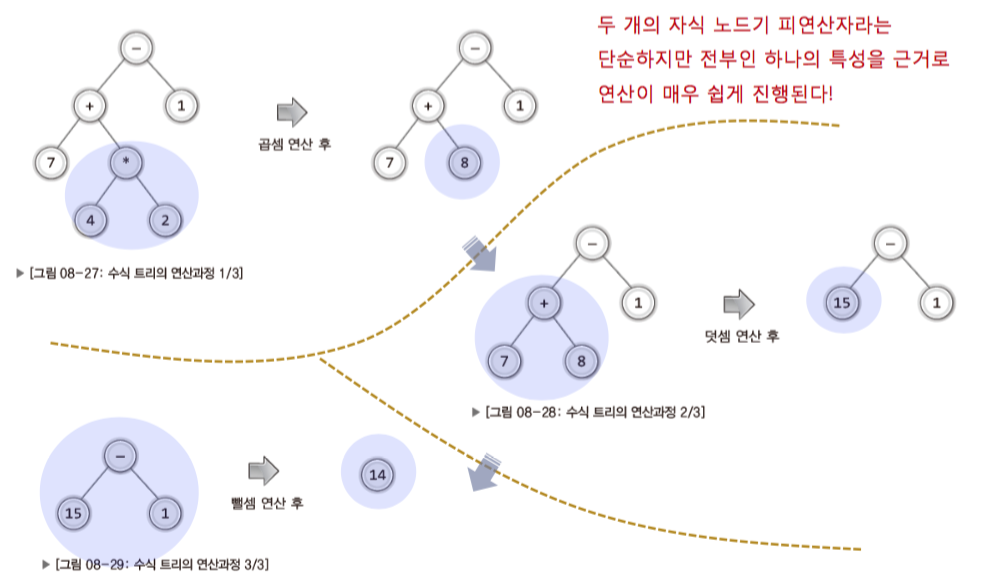
1-2. 이제 진짜 중위 표기법 수식을 가지고 수식 트리를 만들어 보자.
- 일단 바로 수식트리를 만드는 것은 쉽지 않다.
- 컴퓨터가 계산하기 쉽게 전에 스택을 이용해서 후위 수식으로 바꾸듯이
- 후위 수식으로 바꾸고 수식트리를 만들 것이다.


/// ADT를 보자
BTreeNode * MakeExpTree(char exp[]); // 이 함수는 수식트리 만드는 함수
// 후위 수식을 받어 수식트리를 만들고 루트 주소 값을 반환
int EvaluateExpTree(BTreeNode * bt); // 수식 트리를 가지고 계산한 값을 반환
void ShowPrefixTypeExp(BTreeNode * bt); // 전위 표기법 방식을 출력
void ShowInfixTypeExp(BTreeNode * bt); // 중위 표기법 방식을 출력
void ShowPostfixTypeExp(BTreeNode * bt); // 후위 표기법 방식을 출력
// 위의 함수는 그냥 수식 트리를 전위, 중위, 후위 탐색하면 각 탐색법에
// 맞게 전위, 중위, 후위 표기법의 수식을 출력할 수 있다.
- 후기 표기법에서 먼저 등장하는 피연산자와 연산자를 가지고 트리 하단부터 윗로 트리를 만들어 간다.
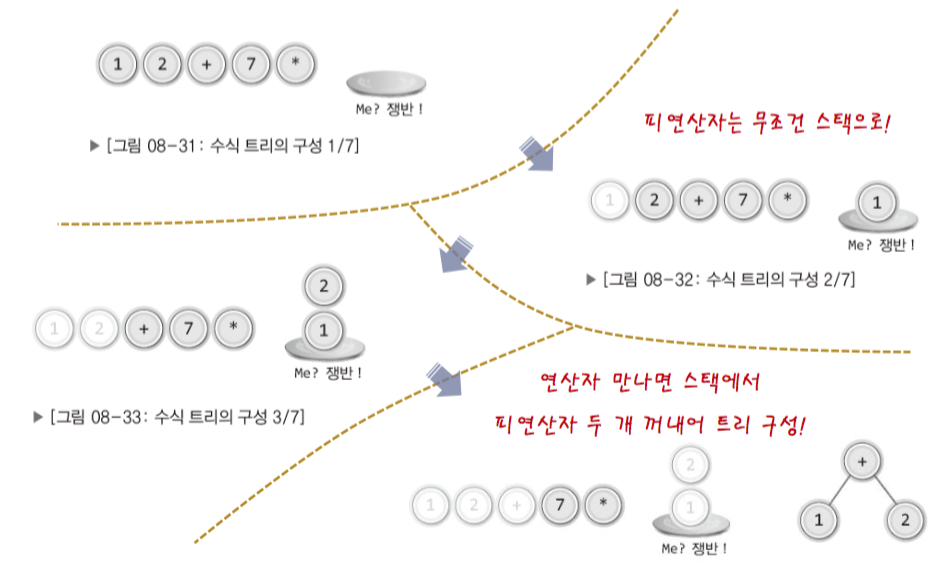
1-3. 후위 표기법을 수식트리로 하는 과정
- 스택을 이용한다.
- 피연산자는 무조건 스택으로
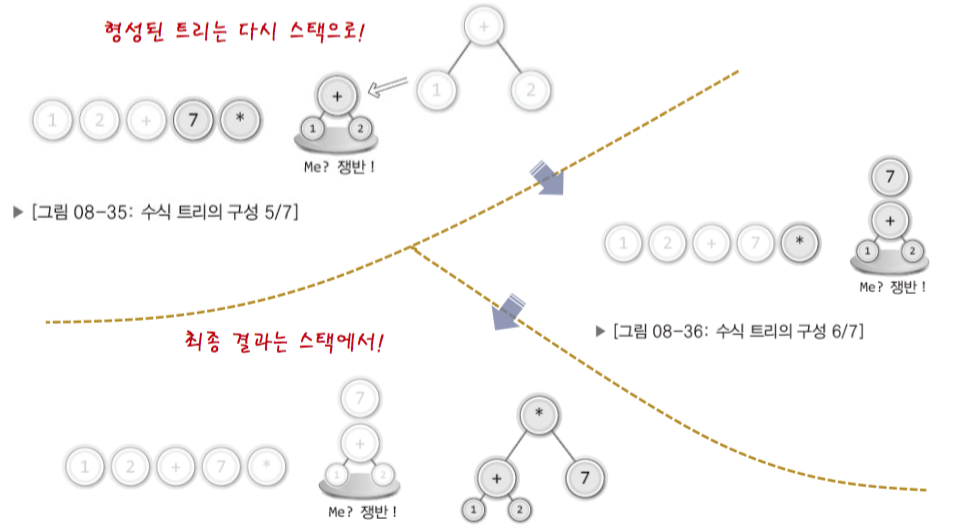
- 연산자를 만나면 트리로 하도 다시 스택으로, 이 과정을 수식의 최대 길이까지 반복한다.
//위의 과정을 코드로 옮겨보자
BTreeNode * MakeExpTree(char exp[])
{
Stack stack;
BTreeNode * pnode;
int expLen = strlen(exp);
int i;
for(i = 0 ; i < expLen ; i++)
{
pnode= MakeTreeNode();
if(!isdigit(exp[i])) // 피연산자라면
{
SetData(pnode, exp[i]-'0') // 정수로 변환을 해서 저장
}
else // 연산자면 트리로 만든다.
{
MakeLeftSubTree(pnode, SPop(&stack));
MakeRightSubTree(pnode, SPop(&stack));
SetData(pnode, exp[i]);
//위 순서대로 한다.
}
// 항상 스택에 푸쉬
SPush(&stack, pnode);
}
return SPop(&stack);
}
- 전위 순회하여 데이터 출력 결과 : 전위 표기법 수식
- 중위 순회하여 데이터 출력 결과 : 중위 표기법 수식
- 후위 순회하여 데이터 출력 결과 : 후위 표기법 수식
// 위의 방식들의 데이터 출력 결과를 가지고 수식트리가 제대로 만들어 졌는지 검증 할 수 있다.
void ShowPrefixTypeExp(BTreeNode * bt)
{
PreoderTraverse(bt, ShowNodeData);
// 전위 표기법 수식 출력
}
void ShowInfixTypeExp(BTreeNode * bt)
{
InoderTraverse(bt, ShowNodeData);
// 중위 표기법 수식 출력
}
void ShowPostfixTypeExp(BTreeNode * bt)
{
PostoderTraverse(bt, ShowNodeData);
// 후위 표기법 수식 출력
}
// 위에 피연산자는 정수로 바꿔서 저장했기 때문에
// 아래와 같이 구현
void ShowNodeData(int data)
{
if(0<= data & data <= 9)
printf("%d ", data); /// 피연산자 출력
else
printf("%c ", data); // 연산자 출력
}
//위를 가지고 main 함수를 구성해보자
int main (void)
{
char exp[] = "12+7*";
BTreeNod * eTree = MakeExpTree(exp);
printf("전위 표기법의 수식: ");
ShowPrefixTypeExp(eTree); printf("\n");
printf("중위 표기법의 수식: ");
ShowInfixTypeExp(eTree); printf("\n");
printf("후위 표기법의 수식: ");
ShowPostfixTypeExp(eTree); printf("\n");
printf("연산의 결과 : %d\n", EvaluateExpTree(eTree));
return 0;
}
/// 위의 main 함수의 결과는
/// 전위 표기법의 수식 : * + 1 2 7
/// 중위 표기법의 수식 : 1 + 2 * 7
/// 후위 표기법의 수식 : 1 2 + 7 *
/// 연산이 결과 : 21
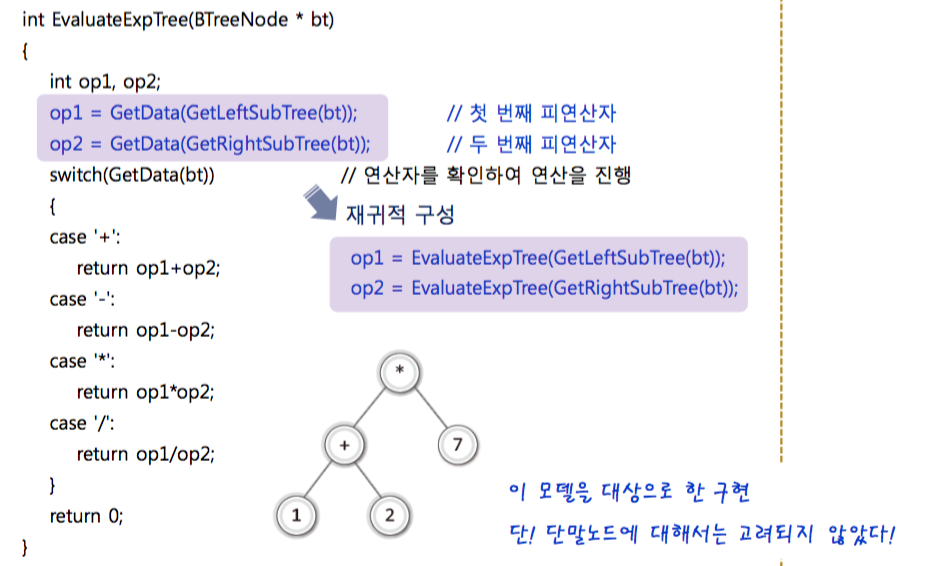
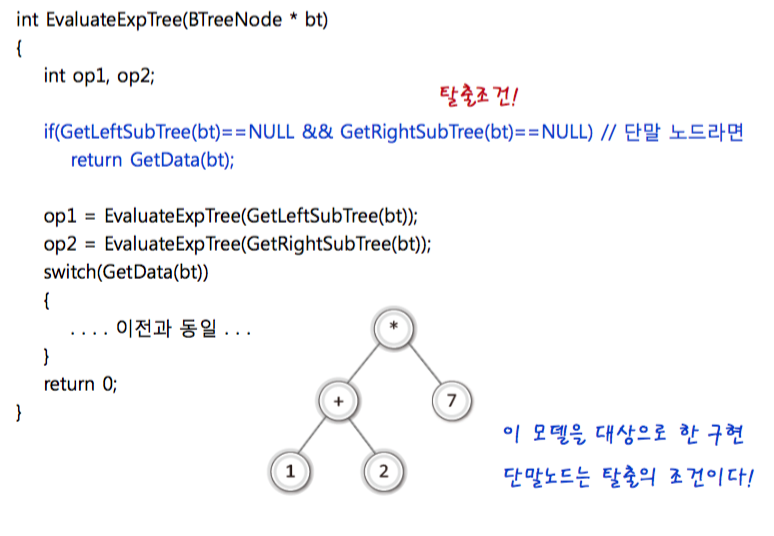
////// 자 그럼 EvaluateExpTree 함수를 코드로 구현해보자