Tree

this refers to 윤성우의 열혈 자료구조.

tree is data structure of Hierarchical Relationship(계층적 관계).

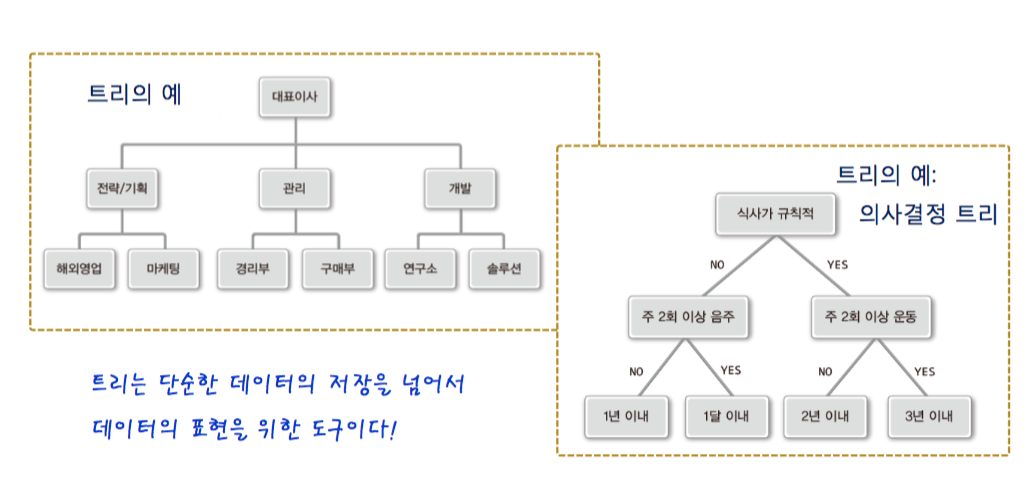
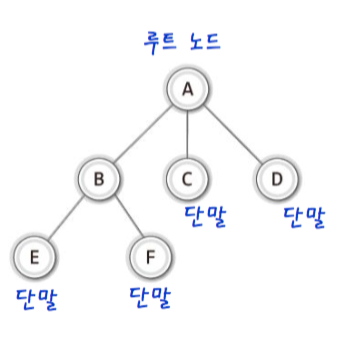
1-1. basic concept of tree

- node(노드) : part of tree(트리의 구성요소), for example A, B, C, D, E, F node.
- edge(간선) : this connect each other node.(서로 다른 노드를 연결하는 선) 
- root node(루트노드) : top node of tree(트리의 최상위 노드). for example A node
- terminal node(단말 노드): this don't connect another node. for example E, F, C, D node (아래로 다른 노드가 연결 안되어 있다. )
- iternal node(내부 노드) : all node except for terminal node,(단말 노드를 제외한 모든 노드) for example A, B node

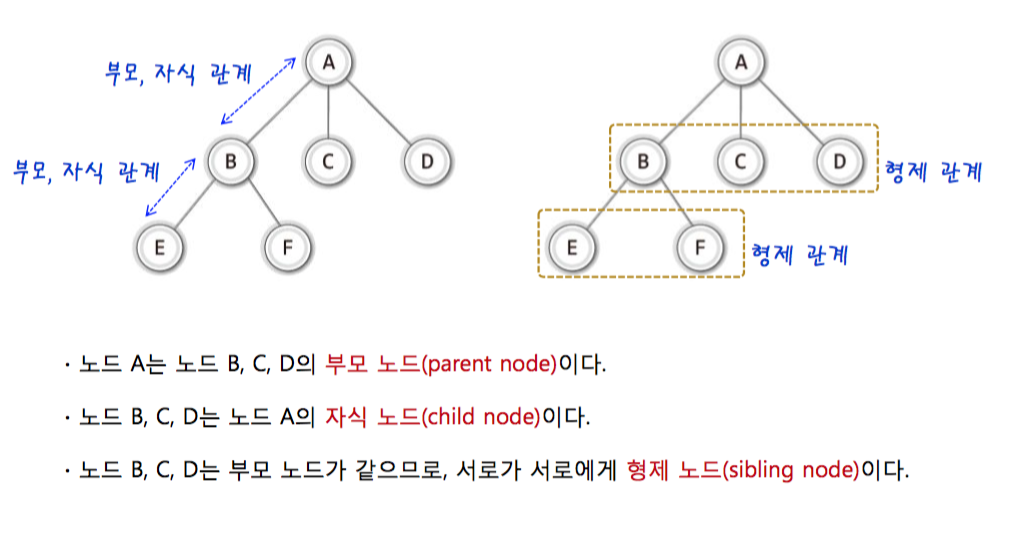
1-2. relationship of tree node

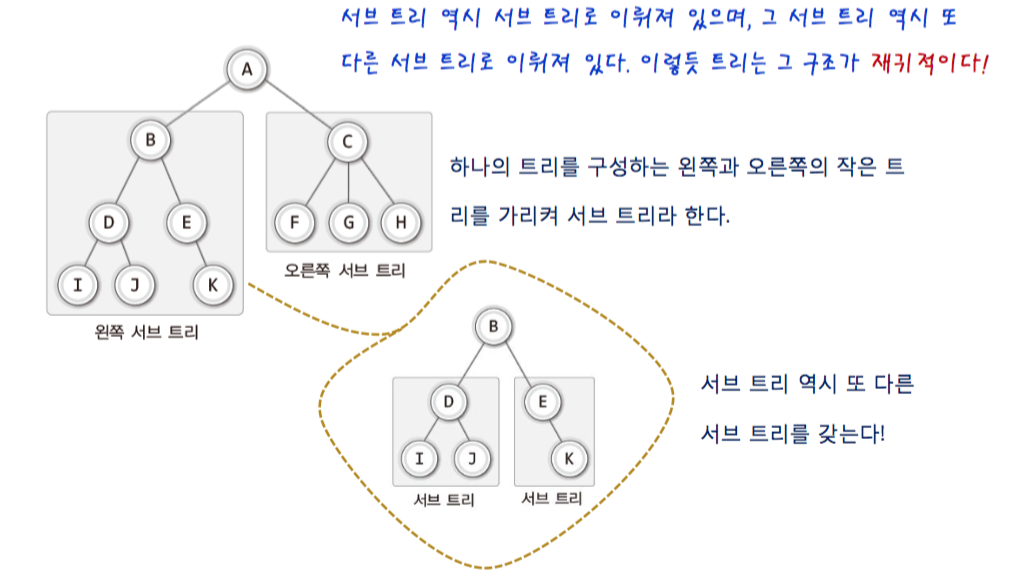
1-3. subtree

- tree is recursive.(트리는 재귀적이다) 그래서 재귀 함수를 많이 이용할 수 있다.

1-4. binary tree

- a node has two children.(하나의 노드는 두개의 자식을 가진다)
- root has two subtree. (루트는 두개의 서브트리를 가지고)
- also, the divied subtree is binary tree.(나누어진 서브트리도 이진트리이다.)
- 트리 및 이진 트리는 구조가 재귀적이다. 즉, 트리와 관련해서는 재귀적 사고와 재귀적을 구현하면 좋다. 

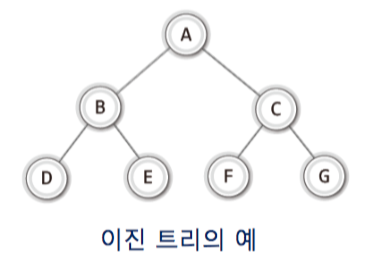
1-5. binary tree & null node

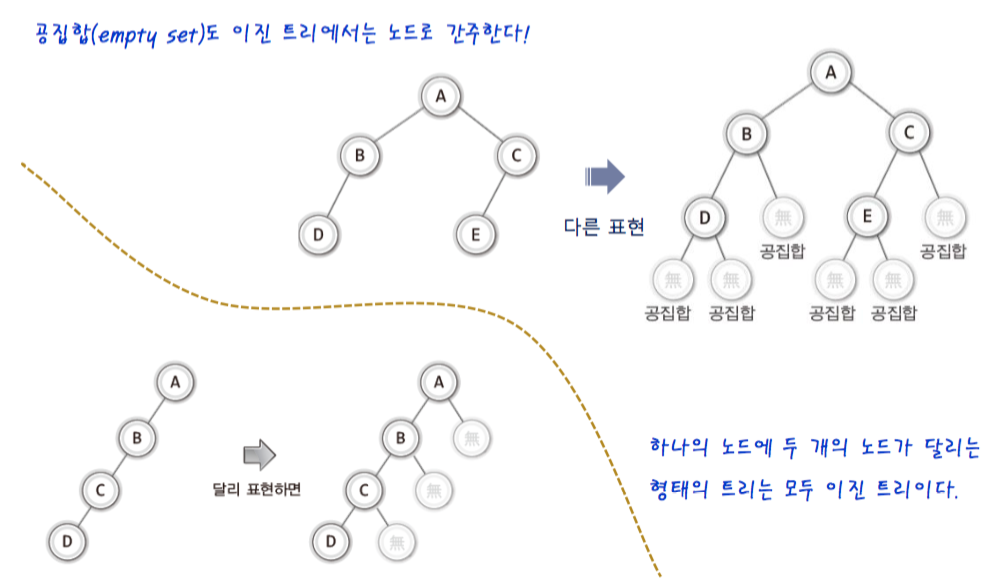
1-6. height & level of tree

- full binary tree is that node is full in tree.(포화 이진 트리는 모든 레벨에 노드가 꽉 차있다.)
- complete binary tree is from the up to the down & from the right to the left.
- 완전 이진 트리는 나중에 힙에 사용이 되는 트리이기도 하다. 
- 노드가 채워지는 순서가 있다 위에서 아래로 그리고 오른쪽에서 왼족으로 노드가 채워진다.

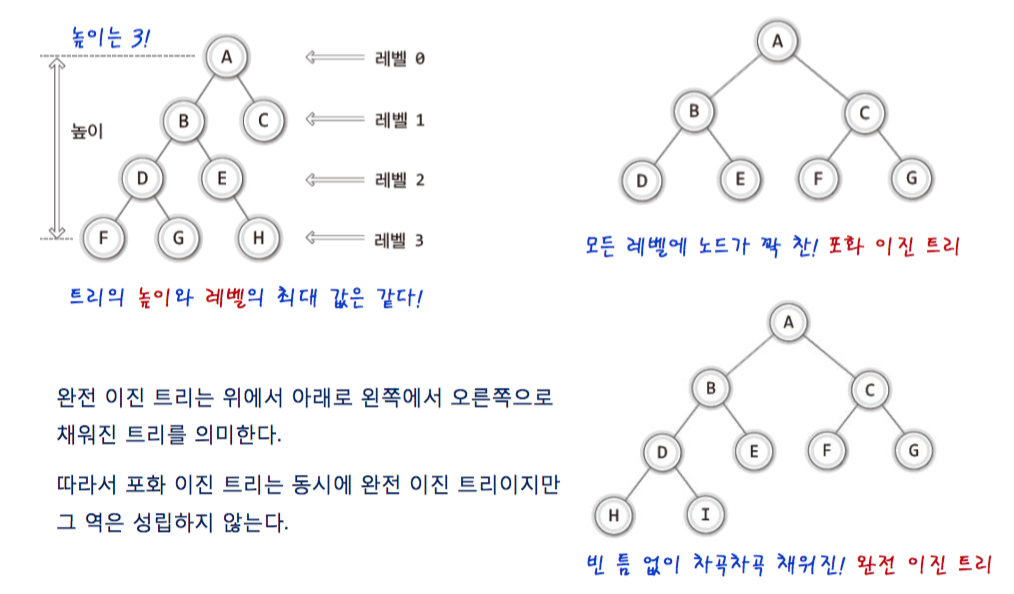
1-7. implementation of tree

- 트리는 배열 or 리스트 기반으로 구현을 한다.

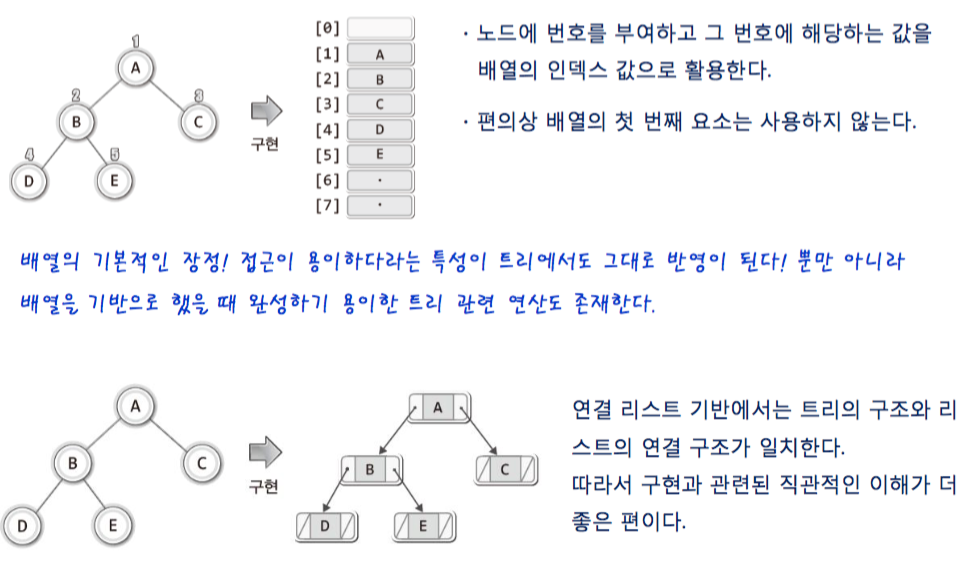
1-8. now source code using LinkedList.

- tree node's structure
- 트리의 모든 노는 직접 간접적으로 연결이 되어 있어 root 주소 값만 알아도 이진 트리 전체를 알 수 있다.
- 하나의 노드는 논리적으로는 이진트리이다. 즉 노드는 이진트리이다. 

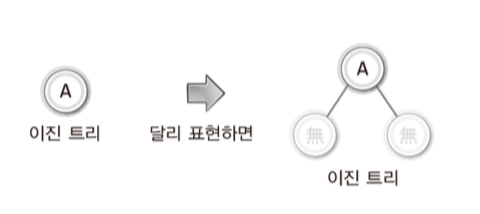
// 이진 트리의 노드 모양
typedef struct _bTreeNode
{
    BTData data;
    struct _bTreeNode * left;
    struct _bTreeNode * right;
} BTreeNode;

- 함수를 통해 접근을 하자. 노드에 직접 접근 보다는

- tree function

- 위의 함수를 이용한 메인 함수 부분

int main(void)
{
    BTreeNode * ndA = MakeBTreeNode(); // 노드 A 생성
    BTreeNode * ndB = MakeBTreeNode(); // 노드 B 생성
    BTreeNode * ndC = MakeBTreeNode(); // 노드 C 생성
    
    위의 노드를 SetData를 통해 데이터를 채운다. 
    
    // A노드에 왼쪽 자식으로 B 노드 연결
    MakeLeftSubTree(ndA, ndB);
    
    
    // A노드에 오른쪽 자식으로  C 노드 연결
    MakeRightSubTree(ndA, ndC);
}

// 앞에 만든 함수를 이용해서 트리를 구현하고 있다. 

// 자 이제 본격적인 이진 트리의 ADT들을 만들어 보자 
BTreeNode * MakeBTreenNode(void)
{
        BTreeNode * nd = (BTreeNode * )malloc(sizeof(BTreeNode));
        nd -> left = NULL;
        nd -> right = NULL;
        return nd;
}

BTData GetData (BTreeNode * bt)
{
        return bt -> data;
}

void SetData(BTreeNode * bt, BTData data)
{
    bt -> data = data;
}

BTreeNode * GetLeftSubTree(BTreeNode *  bt)
{
    return bt -> left;
}

BTreeNode * GetRightSubTree(BTreeNode *  bt)
{
    return bt -> right;
}

void MakeLeftSubTree(BTreeNode * main, BTreeNode * sub)
{
    if(main -> left != NULL)
        free(main -> left);    /// 하지만 이거 서브트리가 자식을 가지고 있는경우
                            ///  memory leak이 발생한다. 
                            
    main -> lenf = sub;
}


void MakeRightSubTree(BTreeNode * main, BTreeNode * sub)
{
    if(main -> right != NULL)
        free(main -> right);    /// 하지만 이거 서브트리가 자식을 가지고 있는경우
                            ///  memory leak이 발생한다. 
                            
    main -> right = sub;
}

/// 위의 두개의 함수에서 메모리 누수가 나면 효과적인 방법이 있다 .
// 바로 트리의 traversal를 이용하면 메모리의 누수가 없을 것이다. 


// 위의  ADT를 이용해서 main function를 이용해보자 
int main(void)
{
    BTreeNode * bt1 = MakeBTreeNode(); // 노드 bt1 생성
    BTreeNode * bt2 = MakeBTreeNode(); // 노드 bt2 생성
    BTreeNode * bt3 = MakeBTreeNode(); // 노드 bt3 생성
    BTreeNode * bt4 = MakeBTreeNode(); // 노드 bt4 생성
    
    //위의 노드를 SetData를 통해 데이터를 채운다. 
    SetData(bt1, 1);   //bt1에 1 저장
    SetData(bt2, 2);   //bt2에 2 저장
    SetData(bt3, 3);   //bt3에 3 저장
    SetData(bt4, 4);   //bt4에 4저장
        

    MakeLeftSubTree(bt1, bt2);     // bt2를 bt1의 왼쪽 자식 노드로 만든다. 
    MakeRightSubTree(bt1, bt3);    // bt3를 bt1의 오른쪽 자식 노드로 만든다. 
    MakeLeftSubTree(bt2, bt4);     // bt4를 bt2의 왼쪽 자식 노드로 만든다. 
    
    // bt1의 왼쪽 자식 노드의 데이터 출력
    printf("%d\n", GetData(GetLeftSubTree(bt1)));
    
    // bt1의 왼쪽 자식 노드의 왼쪽 자식 노드의 데이터 출력
    printf("%d\n", GetData(GetLeftSubTree(GetLeftSebTree(bt1))));
    
    return 0;
}


// 출력결과
// 2
// 4

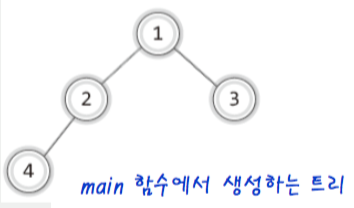
1-9. binary tree traversal

- 세가지 순회방법 : 루트 노드의 방문 순서에 따라, 
- 자식노드 탐색순서는 왼쪽노드 다음 오른쪽 노드이고 O left O right O 여기서 O에 루트노드가 들어간다.
- 중위(inorder), 후위(postorder), 전위(preorder)

1-10. recursive traversal

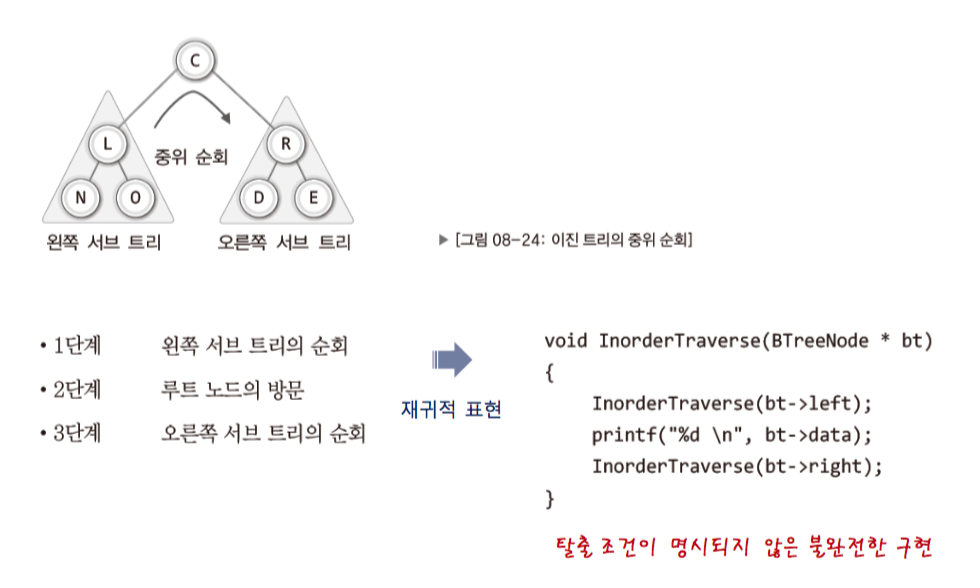
- 위의 함수에 기저 조건을 추가

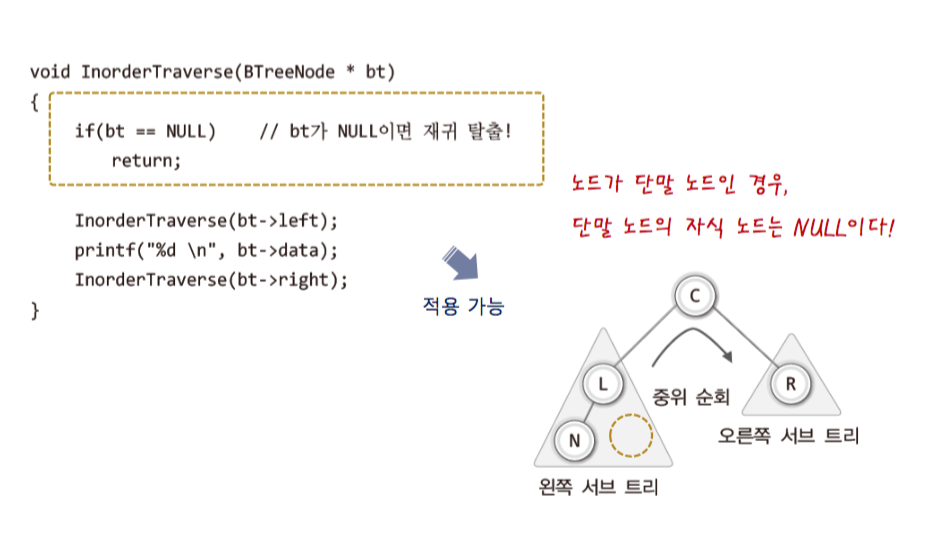
- 아래는 각각의 전위, 후위, 중위 순회를 보여준다.

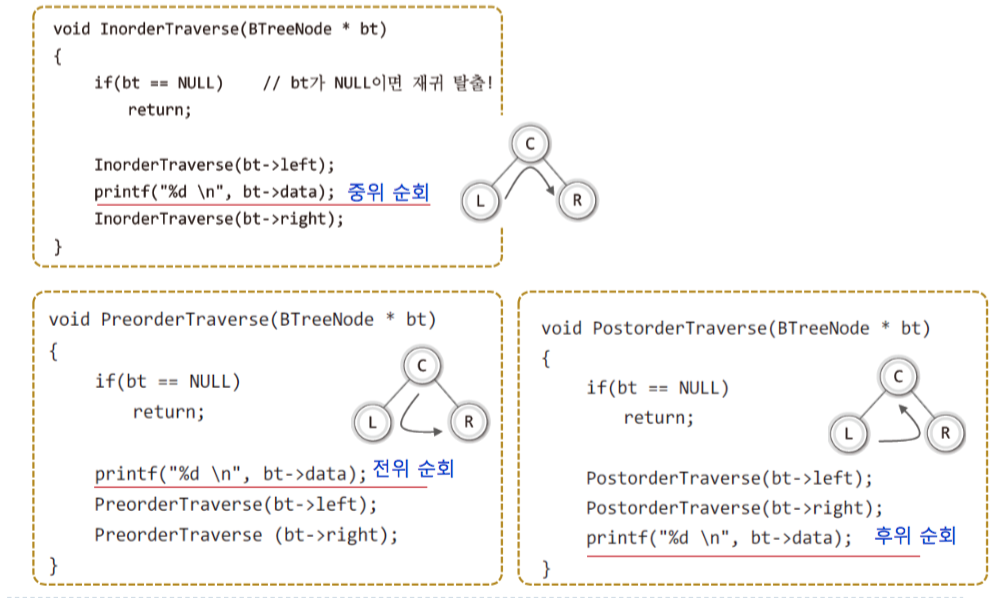
위와 같이 노드를 방문을 하면서 우리는 다양한 작업을 트리에서 할 수 있다.

typedef void VisitFuncPtr(BTData data); // 이런 방식으로 커널에 사용 
// typedef void (*VisitFuncPtr) (BTData data);
// 위는 함수 포인터의 데이터 타입 설정 

void InOrderTraverse(BTtreeNode * bt, VisitFuncPtr action)
{
        if(bt == NULL)
            return ;
    
    InOrderTraverse(bt -> left, action);
    action(bt -> data);
    InOrderTraverse(bt -> right, action);
}

void ShowIntData(int data)
{
    printf("%d ", data);
}

// 위와 같은 방식을 활용하여 좀더 트리를 다양하게 이용을 할 수가 있다. 